হ্যাকাররাই তা হলে দাপিয়ে বেড়াবে? তাদের জন্য তা হলে সব সময়ই আমাদের দুশ্চিন্তায় কাটাতে হবে?
গত কয়েক মাসে, লকডাউন ও অতিমারির কারণে কাজ হারিয়েছেন বহু মানুষ। কিন্তু বিশেষ কয়েকটি জীবিকায় যাঁরা রয়েছেন, তাঁদের পসার কিন্তু বেশ ফুলে ফেঁপে উঠেছে। সেই কয়েকটি পেশার অন্যতম ‘হ্যাকিং’।
গৃহবন্দি মানুষ যত বেশি করে ঝুঁকেছেন অনলাইন কেনাকাটার দিকে, ততই বাড়ছে হ্যাকারদের কাজ কারবার। এরা জেনে ফেলছে আমাদের গোপন পাসওয়ার্ড, কখনও খালি করে দিচ্ছে আমার, আপনার ব্যাঙ্কের অ্যাকাউন্ট, কখনও বা হানা দিচ্ছে ভ্যাকসিন প্রস্তুতকারী প্রতিষ্ঠানের সার্ভারে।
খুব স্বাভাবিক ভাবেই আমাদের মনে প্রশ্ন জাগছে, এমনটা কি চলতেই থাকবে? এমন দিন কি আসবে না, যখন হ্যাকারদের ভয় ছাড়াই আদানপ্রদান করা যাবে গোপন বার্তা আর নির্ভয়ে করা যাবে সব রকমের অনলাইন লেনদেন?
সেই দিনেরই আশা দেখাচ্ছে কোয়ান্টাম ক্রিপ্টোগ্রাফি। যার মূল দাবিই হল, কোনও গোপন তথ্যকে পুরোপুরি গোপন রাখতে পারা ও সম্পূর্ণ গোপনীয়তার সঙ্গে এক স্থান থেকে আর এক স্থানে সেই গোপন তথ্যকে পাঠানোর ক্ষমতা।
তাই এটা মনে হওয়া খুবই স্বাভাবিক, কোয়ান্টাম ক্রিপ্টোগ্রাফি ব্যবহার করে আমরা যদি অদূর ভবিষ্যতে সম্পূর্ণ গোপনীয়তার সঙ্গে তথ্যের আদানপ্রদান শুরু করি, তা হলে হ্যাকাররা কর্মহীন হয়ে যাবে।
কিন্তু সত্যিই কি সেটা হবে? এই প্রশ্নের উত্তর জানতে হলে আমাদের জেনে নিতে হবে হ্যাকার বা কোডব্রেকার কাদের বলা হয়? তারা কী ভাবে কাজ করে? কী ভাবেই বা আমরা প্রতিহত করতে পারি তাদের গোপন তথ্য জেনে ফেলার কায়দা কসরত?

নয়ডার জেপি ইনস্টিটিউট অব ইনফর্মেশন টেকনোলজির গবেষণাগারে অধ্যাপক অনির্বাণ পাঠক। ছবি- লেখকের সৌজন্যে।
মানুষ যখন থেকে বুঝতে শিখেছে, সব কথা বা সব তথ্য সকলের জানা শ্রেয় নয়, তখন থেকেই শুরু করেছে তথ্য গোপন রাখার নানা চেষ্টা। জন্ম হয়েছে একটি বিশেষ চর্চার। যার পোশাকি নাম ‘ক্রিপ্টোগ্রাফি’।
একদল লোক চিরকাল চেষ্টা করেছে কোনও পদ্ধতি বা সূত্র ব্যবহার করে তথ্য গোপন রাখার। আর একদল লোক চেষ্টা করেছে অন্যের গোপন তথ্যাদি জেনে ফেলার। প্রথম দলের লোকদের বলা হয় ‘ক্রিপ্টোগ্রাফার’। আর দ্বিতীয় দলের লোকদের বলা হয় ‘ক্রিপ্টোলজিস্ট’ বা ‘কোডব্রেকার’।
রোজকার জীবনে আমরা যাদের ‘হ্যাকার’ বলি, তারা আসলে কোডব্রেকার। যারা কম্পিউটার বিজ্ঞান ও গণিতে পারদর্শী। তাদের আবিষ্কৃত পদ্ধতি ব্যবহার করে আমার আপনার গোপন তথ্যাদি জেনে ফেলার চেষ্টা চালিয়ে যাচ্ছে কিছু লোক। ফলে, আমরা বলতে পারি, সব হ্যাকারই ক্রিপ্টোলজিস্ট নয়। কিন্তু সব ক্রিপ্টোলজিস্টই হ্যাকার (অন্তত ‘এথিক্যাল হ্যাকার’)।
কোডব্রেকার মানেই কিন্তু খারাপ লোক নয়। একটি উদাহরণ দিলে বিষয়টি স্পষ্ট হবে। আমরা সব সময় চাইব, আমাদের দেশের সেনাবাহিনীর মধ্যে যে কথাবার্তা হচ্ছে তা গোপন রাখতে। কারণ, তাতেই দেশের মঙ্গল। একই সঙ্গে আমরা যদি প্রতিবেশী দেশের সেনাবাহিনীর নিজেদের মধ্যে চালাচালি করা গোপন সঙ্কেত পড়ে ফেলতে পারি, তা হলে অনেক আক্রমণ প্রতিহত করা যাবে। আগাম প্রস্তুতি নেওয়া যাবে। তাতেও দেশের মঙ্গল।
সেটাই হয়েছিল দ্বিতীয় বিশ্বযুদ্ধের সময়, যখন এলান ট্যুরিং ও অন্যরা ভেঙে ফেলেছিলেন হিটলারের সাঙ্কেতিক বার্তা। যা প্রভাবিত করেছিল দ্বিতীয় বিশ্বযুদ্ধের ফলাফল ও সময়কালকে। সাহিত্যিক এডগার এলান পো-ও ছিলেন এক জন কোডব্রেকার। তিনি বিশ্বাস করতেন, কোনও কোডই এমন নয়, যা ভাঙা যায় না। কোনও কোনও সাঙ্কেতিক বার্তার পাঠোদ্ধার করা সহজ। কোনওটির পাঠোদ্ধার করা কঠিন। এই ধারণাটি সম্পূর্ণ ভাবে বদলে যায় গত শতাব্দীর সাত আর আটের দশকের কয়েকটি ঘটনাপ্রবাহে। সেই গল্প দিয়েই মূল প্রসঙ্গে আসা যাক।
কোয়ান্টাম ক্রিপ্টোগ্রাফির জন্মবৃত্তান্ত
সেটা ১৯৭৯ সালের অক্টোবর। পুয়ের্তো রিকোর রাজধানী সৈকত শহর সান জুয়ানে ক্যারিবিয়ান সাগরে একা সাঁতার কাটছিলেন গিলে ব্রাসার্দ। সেখানে গিয়েছিলেন আইইইই-র একটি সম্মেলনে। হঠাৎ ওঁর খুব কাছে এসে সাঁতার কাটতে লাগলেন এক জন। আর শোনাতে শুরু করলেন একটি গল্প। ওঁর এক সহপাঠীর কথা। যাঁর নাম স্টিফেন ওয়েজনার। তিনি নাকি এক যুগ আগে ১৯৬৮ সালে কোয়ান্টাম মেকানিক্সের সূত্র ব্যবহার করে এমন একটি পদ্ধতির প্রস্তাব দিয়েছেন, যা দিয়ে কারেন্সি নোট বানালে সেই নোট কেউই জাল করতে পারবে না।
ব্রাসার্দকে অযাচিত ভাবে গল্প বলতে আসা লোকটির নাম- বিজ্ঞানী চার্লস বেনেট। সাঁতার কাটতে কাটতে শুরু হওয়া আলোচনা যখন সৈকতে পৌঁছল তখন দুই বিজ্ঞানীর মস্তিষ্কে আঁকা হয়ে গিয়েছে কোয়ান্টাম ক্রিপ্টোগ্রাফি নিয়ে লেখা প্রথম কয়েকটি গবেষণাপত্রের খসড়া। ভবিষ্যতে যা বদলে দেয় ক্রিপ্টোগ্রাফির জগৎটাকেই। আমূল বদলে দেয় আমাদের তথ্যাদির গোপনীয়তার ধারণা।
কোয়ান্টাম ক্রিপ্টোগ্রাফি বলতে কী বোঝায়? দেখুন ভিডিয়োয়।
গোড়ার দিকে তাঁদের গবেষণাপত্রগুলি ছাপতে বেশ বেগ পেতে হয়েছিল কোয়ান্টাম ক্রিপ্টোগ্রাফির পুরোধাদের।
ওয়েজনার তাঁর বৈপ্লবিক গবেষণাপত্রটি (যার মধ্যে প্রোথিত ছিল আধুনিক কোয়ান্টাম ক্রিপ্টোগ্রাফির বেশির ভাগ ধারণার বীজ) ছাপানোর জন্য পাঠান একটি তথ্যপ্রযুক্তির জার্নালে। যদিও গবেষণাপত্রটি লেখা হয়েছিল পদার্থবিজ্ঞানের পরিভাষায়।
সময়ের থেকে এগিয়ে থাকা গবেষণাপত্রটি প্রত্যাখ্যাত হয়ে শীতঘুমে চলে যায় প্রায় দেড় দশকের জন্য। শেষমেশ পুনর্জীবন পায় দুই বিজ্ঞানীর সাঁতারপর্বের পর। প্রকাশিত হয় ১৯৮৩-তে। ব্রাসার্দ আর বেনেটের পক্ষেও খুব সহজ হয়নি তাঁদের শুরুর ধারণাগুলিকে প্রকাশ করা। শেষমেশ ১৯৮৪-তে বেঙ্গালুরুর একটি সম্মেলনের কার্যবিবরণীতে প্রকাশিত হয় বেনেট ও ব্রাসার্দের সাঁতার কাটতে কাটতে এঁকে ফেলা গোপন চাবিকাঠি (‘কি’) বিতরণ পদ্ধতিটি। যা আজ ‘বিবি-৮৪’ পদ্ধতি নামে যথেষ্টই পরিচিত। বিভিন্ন দিক থেকেই এই পদ্ধতিটি ছিল তার আগেকার অনুসৃত চাবিকাঠি বিতরণের সবক’টি পদ্ধতি থেকেই স্বতন্ত্র।
পদ্ধতিটির স্বতন্ত্র বৈশিষ্ট্যগুলির মধ্যে মূল বৈশিষ্ট্যটি ছিল নিঃশর্ত গোপনীয়তা দিতে পারার ক্ষমতা। যা সর্বদাই কাম্য। কিন্তু যা দিতে সনাতনী (‘ক্লাসিকাল’) বিজ্ঞান অক্ষম। বিষয়টি ভাল করে বোঝার জন্য আগে জেনে নেওয়া যাক, 'নিঃশর্ত গোপনীয়তা' বলতে আমরা কী বুঝি?
নিঃশর্ত গোপনীয়তা বনাম শর্তসাপেক্ষ গোপনীয়তা
দাম্পত্যকলহ নিয়ে গল্প উপন্যাসের শেষ নেই। ধরা যাক, এলা ও বাপি (পোশাকি ক্রিপ্টোগ্রাফির ভাষায়, এলিস ও বব) হল এমনই একটি কলহপ্রবণ দম্পতি। যাঁদের বিচ্ছেদ হয়ে গিয়েছে। কিন্তু দু’জনই দু’জনের উপর এতটাই রেগে আছেন যে কেউ কারও মুখ দেখতে চান না। একে অন্যের বন্ধুদেরও বিশ্বাস করেন না। এলা ও বাপি এখন ঠিক করেছেন টস করে স্থির করা হবে, ওঁদের বাড়িটি কে পাবেন? কেউ যেহেতু কারও মুখ দেখবেন না, তাই ওঁদের দূর থেকেই টস করতে হবে। এখন সমস্যা হল, এলা যদি আগেই বলে দেন, ‘হেড পড়েছে’, বাপি বলবেন ‘সেটাই ছিল আমার বাজি’। আর বাপি যদি আগে বলে দেন, ‘আমার বাজি হেড’, তা হলে এলা বলতেই পারেন, ‘টেল পড়েছে’!
কী ভাবে দূর থেকে টস করলেও কেউ কাউকে ঠকাতে পারবেন না?
আমরা একটি পদ্ধতি ভাবতে পারি। এলা টস করে কয়েনটি একটি বাক্সের মধ্যে রেখে বাক্সটিতে তালা দিয়ে চাবিটি নিজের কাছে রেখে বাক্সটি বাপির কাছে পাঠিয়ে দিলেন। বাপি সেই বাক্সটি পাওয়ার পর একটি কাগজে তাঁর বাজিটি লিখে পাঠিয়ে দিলেন এলাকে। আর সেটি পাওয়ার পর এলা চাবিটি বাপিকে পাঠিয়ে দিলেন। আপাতদৃষ্টিতে এই পদ্ধতিতে কেউ কাউকে ঠকাতে পারবেন না। কারণ, টসের ফলাফল আর বাজি, দু’টিরই গোপনীয়তা রক্ষা হয়েছে।
কিন্তু একটু ভেবে দেখলেই বোঝা যাবে, এখানে ফলাফলের গোপনীয়তা সন্দেহাতীত ভাবে বা নিঃশর্ত ভাবে গোপন নয়। কেন? একটু খুলে বলি। এখানে এলা ধরেই নিচ্ছেন, বাপি খুব অল্প সময়ের মধ্যে তালাটি ভেঙে বাক্সের মধ্যে রাখা কয়েনটি দেখে নিয়ে সেই মতো নিজের বাজিটি লিখে এলাকে পাঠাতে পারবেন না। তার মানে, বাপির সক্ষমতা অনুমান করে একটি শর্ত আরোপ করা হচ্ছে। তাতে গোপনীয়তা হয়ে যাচ্ছে শর্তসাপেক্ষ। সনাতনী বিজ্ঞান শুধুই আমাদের শর্তসাপেক্ষ গোপনীয়তা দিতে পারে।
কিন্তু কোয়ান্টাম মেকানিক্স দিতে পারে আমাদের নিঃশর্ত গোপনীয়তা বা সন্দেহাতীত গোপনীয়তা। যেহেতু কোয়ান্টাম ক্রিপ্টোগ্রাফির মূল দাবিই হল, নিঃশর্ত গোপনীয়তা দিতে পারা। সেটা কী ভাবে সম্ভব, এখন তার উপর একটু আলোকপাত করা দরকার।
একটি গাণিতিক সমস্যা কতটা জটিল, তা নির্ভর করে আমরা ক’টি ধাপে সমস্যাটির সমাধান করতে পারি, তার উপর। ধরা যাক, আপনি ২টি ৩ অঙ্কের সংখ্যাকে যোগ করছেন। একটি সংখ্যার নীচে অন্যটিকে লিখে ডান দিক থেকে ৩ বার যোগ করলেই হবে। সংখ্যাদু’টি বড় হলে ধাপের সংখ্যাও বাড়বে। বাড়বে সমাধান করার সময়ও। এ বার ভাবুন, আপনি ওই সংখ্যাদু’টিকেই গুণ করছেন। এ বার কিন্তু ধাপের সংখ্যা যোগের থেকে অনেক বেশি হবে। কারণ, নীচের সংখ্যাটির প্রতিটি অঙ্ক দিয়ে উপরের সংখ্যাটিকে গুণ করতে হবে আলাদা ভাবে। তার পর গুণফলগুলিকে যোগ করতে হবে। সংখ্যাগুলি অনেক বড় হলেও আপনি গুণ করতে পারবেন। কারণ, গুণ করার একটি নির্দিষ্ট পদ্ধতি বা ‘অ্যালগরিদম’ আপনার জানা আছে।
এখন ভাবুন, ২টি খুব বড় মৌলিক সংখ্যাকে গুণ করে আপনাকে বলা হল তার উৎপাদকগুলি বার করতে। তার মানে, ওই মৌলিক সংখ্যাগুলি বার করতে হবে। এটি খুবই জটিল সমস্যা। কারণ, কোনও সনাতনী অ্যালগরিদম দিয়েই খুব দ্রুত মৌলিক উৎপাদক বার করা যায় না।
এই ধরনের কঠিন গাণিতিক সমস্যাগুলিই হল চালু আধুনিক ক্রিপ্টোগ্রাফির ভিত্তি। যেখানে একটি গোপন সঙ্কেতের পাঠোদ্ধার করতে হলে একটি কঠিন গাণিতিক সমস্যার সমাধান করতে হয়। যে কাজটি সময়সাপেক্ষ।
এখন ধরুন, একটি সঙ্কেত গোপনে পাঠাতে এমন একটি গাণিতিক সমস্যা ব্যবহার করা হল, আমাদের জানা সেরা অ্যালগরিদম ও সেরা কম্পিউটার ব্যবহার করলেও যেটির সমাধান করতে ২ দিন সময় লাগে। সে ক্ষেত্রে, আমি ধরে নিতে পারি, সঙ্কেতটি অন্তত এক দিনের জন্য নিরাপদ। দীর্ঘমেয়াদি গোপনীয়তা পেতে আমাদের গাণিতিক সমস্যাটির দৈর্ঘ্য বাড়াতে হবে। তার ফলে, বেড়ে যাবে চাবিকাঠির দৈর্ঘ্য।
এই ধরনের গোপনীয়তা শর্তসাপেক্ষ। কারণ, আমরা ধরে নিচ্ছি, এক জন ব্যক্তি যিনি আমার গোপন কথাটি জানতে আগ্রহী, তাঁর কাছে আমার জানা শ্রেষ্ঠ কম্পিউটার ও অ্যালগরিদমের থেকে উন্নততর কম্পিউটার ও অ্যালগরিদম নেই।
মৌলিক উৎপাদকে বিশ্লেষণ, বিযুক্ত সূচক (‘ডিসক্রিট লগারিদম’) এবং এমন সব কঠিন গাণিতিক সমস্যার ভিত্তিতেই চালু ক্রিপ্টোগ্রাফির প্রতিষ্ঠা। পক্ষান্তরে, কোয়ান্টাম ক্রিপ্টোগ্রাফি গোপনীয়তা রক্ষা করে প্রকৃতির সূত্রগুলিকে ব্যবহার করে। যার অর্থ, কোনও গাণিতিক সমস্যার জটিলতা ব্যবহার না করেই। তাই কোয়ান্টাম ক্রিপ্টোগ্রাফিই তথ্যের নিরাপত্তা দিতে পারে নিঃশর্ত ভাবে।
১৯৯৪ সালে পিটার শোর একটি কোয়ান্টাম অ্যালগরিদমের প্রস্তাব দেন। যা অনেক কম ধাপে অর্থাৎ, অনেক কম সময় সমাধান করতে পারে দু’টি কঠিন সমস্যা। মৌলিক উৎপাদকে বিশ্লেষণ ও বিযুক্ত সূচক।
এই ২টি গাণিতিক সমস্যার জটিলতার উপরেই প্রতিষ্ঠিত যথাক্রমে ‘আরএসএ’ এবং ‘ডিফি হেলম্যান’ নামে খুবই প্রচলিত সনাতনী ক্রিপ্টোগ্রাফির পদ্ধতি।
তাই উপযুক্ত মাপের কোয়ান্টাম কম্পিউটার উপলব্ধ হওয়া মাত্রই ক্রিপ্টোগ্রাফির এই ২টি পদ্ধতিতে পাঠানো কোনও সঙ্কেতের আর কোনও গোপনীয়তা থাকবে না।
এটা ঠিকই, আজ আমাদের হাতে তেমন বড় মাপের কোয়ান্টাম কম্পিউটার নেই। কিন্তু আমরা আজকের পাঠানো সনাতনী সঙ্কেতের অনুলিপি বানিয়ে রাখতে পারি আর ভবিষ্যতে যখন উন্নত মানের কোয়ান্টাম কম্পিউটার আসবে, তখন সঙ্কেতের মধ্যে লুকিয়ে থাকা গোপন বার্তা পড়ে ফেলতে পারব।
সব রাষ্ট্রেরই এমন অনেক গোপন তথ্য থাকে, যা দীর্ঘমেয়াদি গোপনীয়তা দাবি করে। তাই এই ধরনের গোপন তথ্যাদির আদানপ্রদানের জন্য নিঃশর্ত ভাবে গোপনীয়তা দিতে সক্ষম কোয়ান্টাম ক্রিপ্টোগ্রাফির পদ্ধতিগুলির ব্যবহারই শ্রেয়।
কোথা থেকে আসে শর্তহীন গোপনীয়তা?
তথ্যের শর্তহীন নিরাপত্তা আসে প্রকৃতির কয়েকটি নীতি থেকে। কোয়ান্টাম কম্পিউটার থেকে কোয়ান্টাম ক্রিপ্টোগ্রাফি, সব কিছুরই মূলে আছে ‘কিউবিট’ বা ‘কোয়াণ্টাম বিট’। যা একটি দ্বিস্তর ব্যবস্থা।
ধরা যাক, স্তর ২টিকে আমরা চিহ্নিত করলাম যথাক্রমে ‘০’ এবং ‘১’ দিয়ে। সনাতনী বলবিদ্যার নিয়়মানুসারে কোনও একটি নির্দিষ্ট সময়ে এই ব্যবস্থাটি বিদ্যমান থাকবে ০ অথবা ১ স্তরে এবং পরিমাপ করলে শুধু সেই স্তরেই পাওয়া যাবে। কিন্তু কোয়ান্টাম মেকানিক্সের নিয়মানুসারে ব্যবস্থাটি একই মুহূর্তে ০ এবং ১, উভয়েই বিদ্যমান থাকতে পারে।
একটি অর্ধস্বচ্ছ কাচের টুকরো তার উপরে পড়া আলোকে আংশিক ভাবে প্রতিফলিত ও আংশিক ভাবে প্রতিসৃত করে। তাই আমরা বিজ্ঞানের পরিভাষায় এমন কাচের টুকরোকে বলি ‘বিম-স্প্লিটার’ (beam-splitter) বা রশ্মি-বিদারক।
ধরা যাক, আলোর একটি মাত্র কণা পড়ল একটি বিম-স্প্লিটার (beam-splitter)-এর উপর। তখন আলোকণাটি একই সঙ্গে প্রতিফলিত ও প্রতিসৃত হবে।
এ বার যদি আমরা দু’টি শনাক্তকরণ যন্ত্র (‘ডিটেক্টর’) রেখে দিই, একটি প্রতিফলনের দিকে, অন্যটি প্রতিসরণের দিকে, তা হলে কিন্তু ২টি শনাক্তকরণ যন্ত্র একই সময়ে ওই আলোর কণাকে শনাক্ত করতে পারবে না। একটি আলোক কণা যে কোনও একটি শনাক্তকরণ যন্ত্রে ধরা পড়বে। আর এই ধরা পড়াটি হবে সম্পূর্ণ এলোমেলো বা ‘র্যান্ডম’ একটি ঘটনা। অবস্থা পরিমাপ করতেই সেটির পতন হবে ২টি সম্ভাব্য স্তরের মধ্যে একটি স্তরে।
এই ধারণাটি কাজে লাগিয়েই নকল করা যায় না, এমন টাকা বানানোর প্রস্তাব দেন ওয়েজনার। খুব সহজ ভাবে বললে, ওঁর প্রস্তাবটি ছিল এই রকম-
প্রতিটি কারেন্সি নোটে থাকে একটি করে স্বতন্ত্র সংখ্যা। সেই সংখ্যার বদলে যদি আমরা কয়েকটি করে কিউবিট বসিয়ে দিই তা হলে কেউ নোটটি নকল করার চেষ্টা করলেই কিউবিটগুলির অবস্থার পতন হবে। কিউবিটগুলির অবস্থা এমন ভাবে বদলে যাবে যেখান থেকে তাদের আর আগের অবস্থায় ফিরিয়ে আনা যাবে না। ফলে, ধরা পড়ে যাবে নোট জাল করার প্রচেষ্টা।
অজানা কোয়ান্টাম ব্যবস্থার অনুলিপি বানানো যায় না। তাই কোয়ান্টাম টাকা জাল করা সম্ভব নয়। খুব আকর্ষণীয় হলেও ধারণাটির কোনও বাস্তব ভিত্তি নেই। কারণ, কোয়ান্টাম ব্যবস্থাগুলি বড়ই ভঙ্গুর। আপনি পরিমাপ করার চেষ্টা না করলেও পরিবেশের সংস্পর্শে এসে কিউবিটগুলির অনিয়ন্ত্রিত পতন হতে পারে।
কিউবিটগুলির এই অনভিপ্রেত পতন বা পরিবর্তন রোধ করার কোনও পদ্ধতি আমাদের জানা নেই বলেই আমরা এখনও পর্যন্ত বানিয়ে ফেলতে পারিনি কোনও মস্ত বড় কোয়ান্টাম কম্পিউটার। যা দিয়ে শোরের পদ্ধতি বা অনুরূপ কোনও পদ্ধতি ব্যবহার করে ভেঙে ফেলা যাবে সনাতন পদ্ধতিতে পাঠানো সঙ্কেতের গোপনীয়তা।
ফিরে আসা যাক বিম-স্প্লিটার (beam-splitter)-এর প্রসঙ্গে। এখন যদি আমরা একটির পর একটি আলোর কণা পাঠাতে থাকি আর প্রতিফলনের দিকের যন্ত্রে ধরা পরলে ০ লিখি আর অন্যথায় লিখি ১, তা হলে আমরা পেয়ে যাব ০ এবং ১-এর এলোমেলো শৃঙ্খলা। এমন এলোমেলো শৃঙ্খলা অনেক কাজে লাগে। রাজ্য লটারি থেকে ক্যাসিনো, আবহাওয়া বিভাগ থেকে বিজ্ঞানী, সকলেরই দরকার এমন এলোমেলো সংখ্যার শৃঙ্খলা। কিন্তু সনাতনী বিজ্ঞান আমাদের দিতে পারে না সত্যিকারের এলোমেলো সংখ্যার শৃঙ্খলা।
এমন এলোমেলো সংখ্যার শৃঙ্খলার কার্যকারিতা আরও বেড়ে যায়, যদি দু’টি ভিন্ন স্থানে থাকা দু’জন মানুষের কাছে থাকে একই রকমের এলোমেলো সংখ্যার শৃঙ্খলা। তারা এই সংখ্যাটিকে চাবিকাঠি হিসাবে ব্যবহার করে গোপন ভাবে তথ্যের আদানপ্রদান করতে পারে।

গ্রাফিক তথ্য- লেখকের সৌজন্যে। গ্রাফিক- নিরূপম পাল।
কোয়ান্টাম মেকানিক্স আমাদের অনুমতি দেয় না অজানা কোয়ান্টাম ব্যবস্থার অনুলিপি বানাতে। এরই পোশাকি নাম- ‘নো ক্লোনিং থিওরেম’।
এর সঙ্গে যুক্ত হয় কোয়ান্টাম মেকানিক্সের আরও ২টি বিশেষ নীতি। ১) কিছু কিছু কোয়ান্টাম ব্যবস্থার প্রকৃতি হল অস্থানীয় অর্থাৎ ‘নন-লোকাল’, ২) হাইজেনবার্গের অনিশ্চয়তা তত্ত্ব।
এর একটি উদাহরণ আমাদের অনেকেরই জানা। একটি বস্তুর অবস্থান ও ভরবেগ একই দিকে একই সময়ে সঠিক ভাবে আমরা মাপতে পারি না।
হাইজেনবার্গের অনিশ্চয়তা তত্ত্বের আর একটি রূপ আমাদের প্রতিহত করে উলম্ব ভাবে বা সমান্তরাল ভাবে সমবর্তিত (‘পোলারাইজ্ড’) আলো এবং ৪৫ ডিগ্রি বা ১৩৫ ডিগ্রিতে সমবর্তিত আলোর সমবর্তনের দিশা একই সঙ্গে সঠিক ভাবে নির্ণয় করতে।
নো ক্লোনিং থিওরেম এবং হাইজেনবার্গের অনিশ্চয়তা তত্ত্বের এই বিশেষ রূপটি থেকেই আসে বিবি৮৪ পদ্ধতির সুরক্ষা। সহজ ভাবে বলতে হলে, কোয়ান্টাম মেকানিক্সের উপরোক্ত নীতিগুলো থেকেই আসে নিঃশর্ত গোপনীয়তা।
বিষয়টি সহজ ভাবে বুঝে নিতে এক বার নজর দেওয়া যাক প্রথম ছবির দিকে। দেখা যাচ্ছে, চাবিকাঠিটি জানা থাকলেই পড়ে ফেলা যাবে গোপন বার্তা। কিন্তু তা না হলে গোপন বার্তা সম্পর্কে কিছুই জানা যাবে না।কারণ, উপরোক্ত ছবিতে যোগের নিয়মানুসারে গোপন সঙ্কেতের কোনও একটি সংখ্যা ০ হলে বার্তার সংশ্লিষ্ট অঙ্কটি ০ অথবা ১, উভয়ই হতে পারে। একই কথা প্রযোজ্য গোপন সঙ্কেতের সংখ্যাটি ১ হলেও।এখানে চাবিকাঠিটি হতে হবে একটি এলোমেলো সংখ্যা। তা না হলে কোনও গোপন হানাদার আবিষ্কার করে ফেলতে পারে এমন একটি সূত্র, যেটি অনুসারে চাবিকাঠির অঙ্কগুলি তৈরি হয়। আর সেই সূত্রটি জেনে ফেললেই বার্তাটি আর গোপন থাকবে না।
গোপন বার্তা পাঠাতে আমাদের চাই সত্যিকারের এলোমেলো সংখ্যা। আর সেই সংখ্যাকে প্রেরক ও গ্রহীতার মধ্যে বিতরণ করার একটি পদ্ধতি।
প্রথম কাজটি শুধুই কোয়ান্টাম জগতে সম্ভব। কারণ, সনাতনী বিজ্ঞানের জগতে শুধুমাত্র ছদ্ম এলোমেলো সংখ্যাই বানানো যায়। আর দ্বিতীয় কাজটি নিঃশর্ত গোপনীয়তার সঙ্গে করা যায় শুধুমাত্র কোয়ান্টাম জগতেই।

দু’টি আলোর কণা ‘ফোটন’-এর মধ্যে এনট্যাঙ্গল্ড অবস্থায় এমনই হয়। -ফাইল ছবি।
কোয়ান্টাম ক্রিপ্টোগ্রাফি: কর্মহীন হয়ে যাবে কোডব্রেকাররা?
তাত্ত্বিক ভাবে কোয়ান্টাম ক্রিপ্টোগ্রাফি নিঃশর্ত গোপনীয়তা দিতে পারলেও প্রয়োগের ক্ষেত্রে কোয়ান্টাম ক্রিপ্টোগ্রাফির পরিকল্পনাগুলি বাস্তবায়িত করতে গেলে দরকার হয় বিভিন্ন যন্ত্রাংশের। যেমন, আলোর উৎস। যা দিতে পারে একক আলোর কণা বা এনট্যাঙ্গলড আলোক কণা। শনাক্তকরণ যন্ত্র, বিভিন্ন রকম অর্ধস্বচ্ছ বস্তু যা আংশিক ভাবে আলোকে প্রতিফলিত ও প্রতিসৃত অথবা শোষণ বা আলোর সমবর্তনের দিশার পরিবর্তন ঘটাতে পারে।
এই যন্ত্রাংশগুলোর কোনওটিই পুরোপুরি নিখুঁত নয়। এগুলির খুঁত বা সীমাবদ্ধতাই কোয়ান্টাম হ্যাকার বা কোডব্রেকারদের কর্মহীন হয়ে পড়ার হাত থেকে বাঁচায়। তাদের হাতে তুলে দেয় তথাকথিত নিঃশর্ত ভাবে গোপনে কোড ভাঙার বিভিন্ন পদ্ধতি।
গত দু’দশকে কোয়ান্টাম ক্রিপ্টোগ্রাফির পদ্ধতিগুলিকে আক্রমণ করার জন্য কোয়ান্টাম হ্যাকাররা বিভিন্ন পদ্ধতির প্রস্তাব দিয়েছে, পদ্ধতিগুলির বাস্তবায়ন করেছে। আর এগুলো থেকে বাঁচার পদ্ধতি বার করতে গিয়েই উন্নত হয়েছে কোয়ান্টাম ক্রিপ্টোগ্রাফি।
আমাদের গবেষণার দু’টি পরস্পরবিরোধী অংশ আছে। একটি অংশে আমরা চেষ্টা করি এমন সব পরিকল্পনার প্রস্তাব দিতে, যা আমাদের গোপন কাজগুলি নিঃশর্ত গোপনীয়তার সঙ্গে করতে দেবে। অন্য দিকে আমরা চেষ্টা করি ব্যবহৃত যন্ত্রাংশের সীমাবদ্ধতাকে কাজে লাগিয়ে কোয়ান্টাম পরিকল্পনাগুলিকে আক্রমণ করার।
সাধারণত শনাক্তকরণ যন্ত্রগুলি কাজ করে ‘গায়গার মোড’-এ। যেখানে একটি আলোক কণা থেকে সৃষ্টি হয় অনেকগুলি আলোক কণার। আর তার ফলে সৃষ্টি হয় একটি শক্তিশালী সিগন্যালের, যা আমাদের শনাক্তকরণ যন্ত্র শনাক্ত করতে পারে।
কিন্তু এক জন হ্যাকার উজ্জ্বল আলো পাঠিয়ে সাময়িক ভাবে অন্ধ করে দিতে পারে শনাক্তকরণ যন্ত্রটিকে। তখন শনাক্তকরণ যন্ত্রটি গায়গার মোডে কাজ না করে রৈখিক মোডে কাজ করে। সেই সময় হ্যাকার নিয়ন্ত্রণ করতে পারে কোন শনাক্তকরণ যন্ত্র একটি বিশেষ আলোক কণিকাকে শনাক্ত করবে এবং তার ফলে কোন চাবিকাঠি তৈরি হবে।
আগেই আমরা বিম-স্প্লিটার (beam-splitter)-এর কথা বলেছি। বলেছি গোপন চাবিকাঠিটি হতে হবে একটি এলোমেলো সংখ্যা। এও বলেছি একটি শৃঙ্খলায় ০ এবং ১-এর আবির্ভাব যথার্থ ভাবে এলোমেলো হতে হলে বিম-স্প্লিটার (beam-splitter)-কে সমান সম্ভাব্যতার সঙ্গে তার উপর পড়া আলোক কণাকে প্রতিফলিত ও প্রতিসৃত করতে হবে। এমন বিম-স্প্লিটার (beam-splitter)-কে বলা হয় ৫০:৫০ বিম-স্প্লিটার (beam-splitter)। এমন বিম-স্প্লিটার (beam-splitter) সহজপ্রাপ্য। কিন্তু সমস্যা হল, একটি নির্দিষ্ট তরঙ্গদৈর্ঘ্যের জন্যই একটি বিম-স্প্লিটার (beam-splitter) ৫০:৫০ হিসাবে কাজ করে। এক জন হ্যাকার যদি তরঙ্গদৈর্ঘ্য বদলে দেয় তা হলে তৈরি হওয়া চাবিকাঠিটি সম্পূর্ণ ভাবে এলোমেলো হয়ে যাবে না। ফলে, এক জন হ্যাকার অনুমান করে নিতে পারবে প্রতিফলিত দিকের শনাক্তকরণ যন্ত্রটি সাড়া দিয়েছে নাকি অন্যটি।
হ্যাকিং-এর আর একটি সাধারণ পদ্ধতি হল, শনাক্তকরণ যন্ত্রগুলির সক্ষমতার পার্থক্যকে কাজে লাগিয়ে হ্যাক করা। আগের উদাহরণের ব্যবস্থাটিতে শনাক্তকরণ যন্ত্র ২টির সক্ষমতা শুধুই একটি নির্দিষ্ট সময়ে সমান হয়। এক জন হ্যাকার আলোক কণা প্রক্ষিপ্ত হওয়ার সময় নিয়ন্ত্রণ করতে পারে শনাক্তকরণ যন্ত্র ২টির মধ্যে কোনটি সাড়া দেবে। কোনও একটি মুহূর্তে যেটার সক্ষমতা বেশি, সেটার সাড়া দেওয়ার সম্ভাবনাও বেশি।
ক্রিপ্টোগ্রাফির পরিকল্পনাগুলি বাস্তবায়িত করতে যে যন্ত্রাংশগুলি ব্যবহার করা হয় সেগুলির প্রত্যেকটিই প্রতিফলন করে আর সেই প্রতিফলিত আলোকে বিশ্লেষণ করেই আমরা অনেক তথ্য জানতে পারি।
বলা ভাল, নীরব নয়নের দিকে তাকিয়েই পড়ে ফেলতে পারি অনেক গোপন কথা! গ্রিক মহাকাব্য অনুসারে এর নাম- ‘ট্রোজান হর্স অ্যাটাক’। উপরে বর্ণিত হ্যাকিং কৌশলগুলি সম্পূর্ণ বা আংশিক ভাবে প্রতিহত করার পদ্ধতি আমাদের জানা আছে। কিন্তু কোডব্রেকাররা প্রতিনিয়তই খুঁজে চলেছেন হ্যাকিং-এর নতুন নতুন কৌশল। সেই খোঁজে আমরাও শরিক। যন্ত্রের সীমাবদ্ধতাই কোডব্রেকারদের কর্মহীন হতে দেয়নি।
কোয়ান্টাম ক্রিপ্টোগ্রাফি: চাবিকাঠি বিতরণেই সীমাবদ্ধ?
ছবি-১-এ বর্ণিত পদ্ধতি বা তারই অনুরূপ কোনও পদ্ধতির সাহায্যে বিতরণ করা কোয়ান্টাম চাবিকাঠিটি ব্যবহার করে আমরা গোপন বার্তা আদানপ্রদান করে থাকি। এ ক্ষেত্রে কোয়ান্টাম চাবিকাঠি বিতরণের পরবর্তী ধাপে বার্তা ও চাবিকাঠি যোগ করার পদ্ধতিটি কিন্তু কোয়ান্টাম নয়। অর্থাৎ, গোপনীয়তার সঙ্গে তথ্যাদি আদানপ্রদানের জন্য শুধুই কোয়ান্টাম চাবিকাঠি বিতরণই যথেষ্ট নয়।
যদিও কোয়ান্টাম ক্রিপ্টোগ্রাফির এযাবৎ সাফল্যগুলি গোপনীয়তার চাবিকাঠি বিতরণকেন্দ্রিকই। তবে সবচেয়ে আলোচিত সাফল্যটি উপগ্রহের মাধ্যমে চাবিকাঠি বিতরণ।
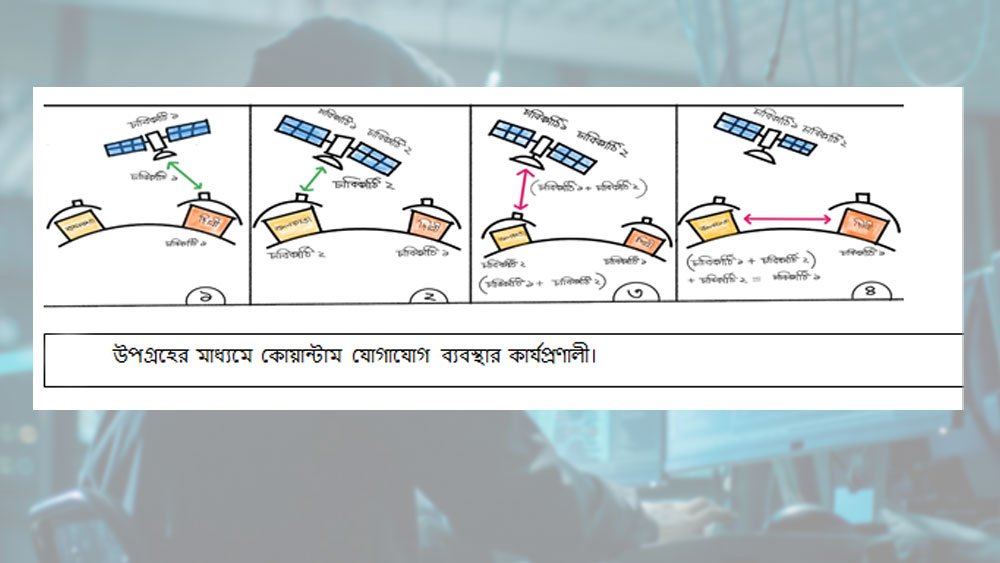
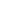
এই ভাবেই উপগ্রহের মাধ্যমে গড়ে তোলা যায় পুরোপুরি সুরক্ষিত কোয়ান্টাম টেলিযোগাযোগ। গ্রাফিক- লেখকের সৌজন্যে।
বিষয়টি সহজ ভাবে বুঝতে আমাদের তাকাতে হবে ছবি-২-এর দিকে। এই উদাহরণে উপগ্রহটি দিল্লির আকাশে থাকাকালীন দিল্লির ঘাঁটির সঙ্গে একটি চাবিকাঠি (চাবিকাঠি ১) ভাগ করে নেয় কোয়ান্টাম সংস্থান ব্যবহার করে। একই ভাবে উপগ্রহটি কলকাতার আকাশে থাকার সময় কলকাতার ঘাঁটির সঙ্গেও একটি চাবিকাঠি (চাবিকাঠি ২) ভাগ করে নেয়। তার পর উপগ্রহটি কলকাতার ঘাঁটিকে ছবি-১-এ বর্ণিত পদ্ধতিতে যোগ করে জানিয়ে দেয় চাবিকাঠি ১ + চাবিকাঠি ২। আর কলকাতার ঘাঁটি সেই যোগফলের সঙ্গে যোগ করে নেয় তার কাছে থাকা চাবিকাঠিটি। ফলে সে পেয়ে যায় চাবিকাঠি ১, যা দিল্লির ঘাঁটির কাছে আগে থেকেই আছে।
ছবি-১-এর মতো করে ভাবলে চাবিকাঠি ১ হল বার্তা আর চাবিকাঠি ২ হল চাবিকাঠি। উপগ্রহের কাজ এখানেই শেষ। পরে গোপন চাবিকাঠি ১ ব্যবহার করে এখন দিল্লি ও কলকাতা নিজেদের মধ্যে গোপন তথ্যের আদানপ্রদান করতে পারে। এখানে ভূপৃষ্ঠের ঘাঁটিগুলির অবস্থান কাল্পনিক, কিন্তু সাম্প্রতিক অতীতে চীন ও অস্ট্রিয়ার মধ্যে এই পদ্ধতিতে ভিডিয়ো কনফারেন্স হয়েছে সফল ভাবে। ভারত-সহ আরও অনেক দেশ এখন এই বিষয়ে বিশেষ ভাবে উদ্যোগী।
ভবিষ্যতের দিকে চেয়ে অনেক গবেষণা হচ্ছে গোপনীয়তার চাবিকাঠি বিতরণের পরের ধাপের কোয়ান্টাম ক্রিপ্টোগ্রাফি নিয়ে। অনেক কাজের জন্যই গোপনীয়তা দরকার। যেমন, অনলাইন ভোটিং, অনলাইন নিলাম ইত্যাদি। এই সংক্রান্ত গবেষণার গুরুত্ব অপরিসীম। কারণ, নিলামের গোপনীয়তা দুর্নীতি কমাতে পারে। ভোটিং-এর গোপনীয়তা গণতন্ত্রকে মজবুত করতে পারে। এই সব কাজের জন্য রয়েছে নানান পরিকল্পনা। ‘আইডিকোয়ান্টিক’ নামে একটি কোম্পানি সুইস সরকারকে একটি কোয়ান্টাম ভোটিং ব্যবস্থা তৈরি করে দিয়েছিল বেশ কয়েক বছর আগে। আমাদের গবেষণাও বহুলাংশে এই ধরনের কোয়ান্টাম পরিকল্পনাগুলির রূপায়ণ চায়। কেন্দ্রীয় বিজ্ঞান ও প্রযুক্তি মন্ত্রকের অর্থানুকুল্যে যে ‘কোয়েস্ট’ প্রকল্পের কাজ চলছে দেশ জুড়ে, আমার গবেষণা তারই অন্যতম। আমার প্রকল্পের নাম- ‘ডিজাইনিং অব ডিভাইসেস অ্যান্ড প্রোটোকলস ফর কোয়ান্টাম হ্যাকিং, র্যান্ডম নাম্বার জেনারেশন অ্যান্ড সিকিওর কমিউনিকেশন’।
কোয়ান্টাম ক্রিপ্টোগ্রাফির বাণিজ্যিক সমাধান এই মুহূর্তে উপলব্ধ। কিন্তু সামরিক, ব্যাঙ্কিং ক্ষেত্রে ব্যবহারের জন্য আমাদের চাই নিজস্ব প্রযুক্তি। তা ছাড়াও ভবিষ্যতে কোয়ান্টাম প্রযুক্তির ব্যবহারে আত্মনির্ভর হওয়ার পাশাপাশি আমরা হতে চাই এই প্রযুক্তির রফতানিকারকও।
সেই উদ্দেশেই ভারত সরকার চালু করেছে ‘কোয়েস্ট’ নামে একটি প্রকল্প। খুব শীঘ্রই শুরু করতে চলেছে একটি জাতীয় মিশন। যার নাম- ‘ন্যাশনাল মিশন অন কোয়ান্টাম টেকনোলজিস অ্যান্ড অ্যাপ্লিকেশন্স' (এনএমকিউটিএ)। এই ২টি প্রকল্পের সাফল্যের উপর অনেকাংশেই নির্ভর করবে ভারতে কোয়ান্টাম প্রযুক্তির ভবিষ্যৎ।
সেই ভবিষ্যৎ নির্মাণে কোয়ান্টাম ক্রিপ্টোলজিস্টদের ভূমিকা কী হবে, সে কথা লেখা আছে রবীন্দ্রনাথের দু’টি লাইনে, ‘গোপন কথাটি রবে না গোপনে, উঠিল ফুটিয়া নীরব নয়নে।’
আমরা এক দিকে তৈরি করতে চাই এমন প্রযুক্তি, যা দিয়ে আমাদের নিজস্ব সব কথা (তথ্যাদি) গোপন রাখা যাবে। অন্য দিকে, আমরা চাই সেই প্রযুক্তি, যার মাধ্যমে অন্যের না বলা গোপন কথাটি তার চোখ দেখেই পড়ে ফেলা যাবে।
লেখক নয়ডার জেপি ইনস্টিটিউট অব ইনফর্মেশন টেকনোলজির পদার্থবিজ্ঞানের অধ্যাপক।
ছবি ও গ্রাফিক: লেখকের সৌজন্যে।